Phase 3: Positioning of nodes

 

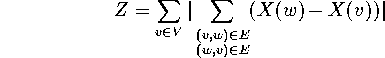
For each node v, absolute coordinates X(v) and Y(v) must be calculated such that (1) R(v) < R(w) implies Y(v) < Y(w) and (2) P(v) < P(w) implies X(v) < X(w). Nodes should not overlap. The layout should be balanced.

Again, we use a layer-by-layer-sweep that is motivated by physical models. As we have seen in section 3, physical simulations often result in very balanced positionings. We start with an arbitrary layout that satisfies conditions (1) and (2). The goal is to minimize

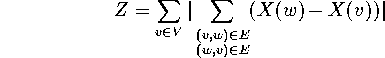
subject to condition (2) and to the condition that nodes must not overlap. Again, this could be solved by standard linear programming methods.

However, a heuristics that is much faster in practice is the rubber band network simulation: the edges pull the nodes like rubber bands. The nodes move horizontally according to the sum of the forces. We define the force

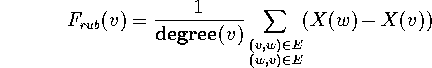
If , we move the node v to the left by the amount , otherwise, we move the node to the right by the amount . Here and denote the left and right neighbor of v in its layer, and d(u,v) is the minimal distance required between nodes u and v. It is easy to see that Z is decreased by these moves.

If the distance between two neighbored nodes of the same layer is minimal, we call the nodes touching. Touching nodes influence each other: if the left is drawn to the right and the right node is drawn to the left, none of both nodes can move. In order to get balance in this case, too, we use regions of nodes: touching nodes belong to the same region iff and . The force at a region is

We move all nodes of the region by . By these moves, Z decreases further.

 
(1)  		 while  Z is not satisfactory small do 

(2)  		  		 for each  layer    from  i = 1 to    n do 

(3)  		  		 		 Calculate all regions of   ;

(4)  		  		 		 Move all nodes according to    of their regions;

(5)  		  		 od 

(6) 		 od 

In the rubber band method, both predecessors and successors influence the position of a node at the same time. As a variation of this method, we can do downward and upward traversals of the layers where only the predecessor or only the successor positions are inspected. This model is more similar to a physical pendulum system. The nodes are like balls, the edges like strings. The uppermost balls are fixed at the ceiling. Then the pendulum system swings until the deflections are balanced. We define the predecessor force for downward traversals

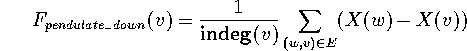
and the successor force for upward traversals

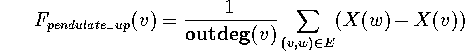
The construction of regions is the same as in the rubber band method. Although experiments show that this pendulum method decreases Z usually much faster than the rubber band method, Z does not decrease in each step. Thus, in practice, we combine both methods [Sa94].

  
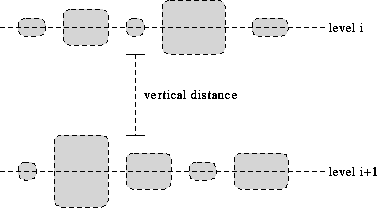
Figure 16: Vertical Positioning at the Levels

[Sa96a] presents a variation of the pendulum method that enforces long edges (sequences of edges in the proper hierarchy) to be strictly vertical. Several other variants of layer-by-layer-sweep to position the nodes of a layer are described in [STT81, EaSu90] and [GKN93].

Y(v) is calculated such that all nodes of the same layer are centered along a horizontal line (Fig. 16). There are two strategies to assign Y(v):

• The vertical distance between layers is a constant : the layer gets the reference line at .
• The vertical distance between two layers depends on the number of overlappings of the projection of the edges to the horizontal. Two different edges and overlap horizontally at one point between and , iff or . The maximal number of overlappings between two layers and at any point can be calculated by a plane sweep in time [Sa96b]. We calculate the reference lines top down: and .

  
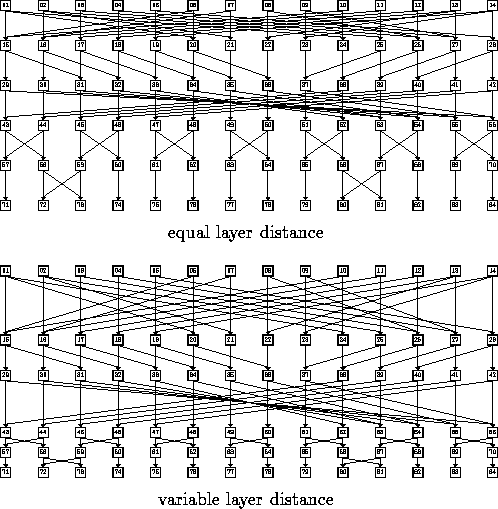
Figure 17: Layer Distance Strategies

The advantage of variable vertical distance between layers is that the angle of edges does not get too small. In particular, inhomogeneous dense graphs are more readable in this way (Fig. 17).