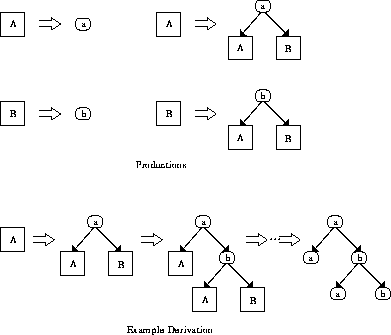
Figure 30: Graph Grammar of Binary Trees
Grouping methods are closely related to graph grammars. While interactive grouping allows the selection of arbitrary sets of nodes, graph grammars are a mechanism for rule based selection of groups. Similar to context free string grammars, graph grammars consist of production rules that describe how a nonterminal node of a graph can be replaced. Fig. 30 shows an example grammar and a graph derivation. The application of a production rule is very similar to the unfolding of a collapsed graph.

Figure 30: Graph Grammar of Binary Trees
It is possible to use the derivation of a graph to control the layout process. In this case, productions are annotated with layout rules. This is called a layout graph grammar [Br95]. For instance, in Fig. 30, there may be a layout rule that the subtree generated from terminal A must always be to the left of the subtree of B, while a general tree layout algorithm may permute the order of the subtrees in order to improve the balance of the tree. Layout graph grammars have been used in several systems [Hi95, BBH94, MSG95, ShMC96].
Since most compiler graphs are structured according to certain rules, layout graph grammars are quite appropriate. This gives syntax trees and control flow graphs a uniform appearance that is easy to recognize. However, since the layout rules are local to a production, a layout method only based on graph grammars does not take the global structure of the graph into account. The results are rarely optimal wrt. used space, edge crossings, etc [Br95].
%