Graphical fisheye views are based on a bijective transformation function h
that describes the mapping of the distances from the focus ![]() in the layout
into distances from the focus
in the layout
into distances from the focus ![]() in the picture.
General rules are:
in the picture.
General rules are:

Figure 33: Graph with Different Views
If h(x) > x for all points x > 0, then the focus point is magnified,
if h(x) < x the focus point is demagnified.
The magnification at distance x from the focus point is
just ![]() .
Transformation functions commonly used for fisheye views are
.
Transformation functions commonly used for fisheye views are
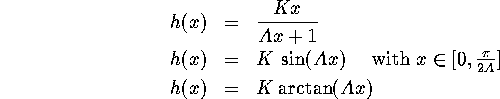
K and A allow to select the magnification at focus point,
and the radius of interest.
The Cartesian fisheye view applies h independently to the x and y directions:
![]() .
Polar fisheye views are based on the polar coordinates. h is applied to
the distance, and the angle of the ray though the origin remains:
.
Polar fisheye views are based on the polar coordinates. h is applied to
the distance, and the angle of the ray though the origin remains:
![]() .
Cartesian views are invariant with respect to horizontal and vertical lines,
thus they are appropriate for orthogonal drawing.
Polar views however are more closer to the fisheye lenses of the photography.
.
Cartesian views are invariant with respect to horizontal and vertical lines,
thus they are appropriate for orthogonal drawing.
Polar views however are more closer to the fisheye lenses of the photography.
The idea of a fisheye is to make the area near the focus point well visible. A distortion near the focus point is often unwelcome. Thus, it is better to use focus areas instead of focus points. Inside the focus area, there is a linear magnification without distortion. The simplest way is to define a transformation in two parts, e.g.:
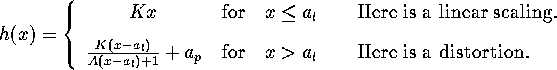
![]() is the radius of the focus area in the layout, and
is the radius of the focus area in the layout, and
![]() is the radius of the focus area in the picture.
With this simple method, we get a focus square for Cartesian fisheye views
and a focus circle for polar fisheye views.
Recently, fisheye views with arbitrary focus polygons were
developed [FoKe96].
These methods are more complex and require the calculation of
Voronoi diagrams.
is the radius of the focus area in the picture.
With this simple method, we get a focus square for Cartesian fisheye views
and a focus circle for polar fisheye views.
Recently, fisheye views with arbitrary focus polygons were
developed [FoKe96].
These methods are more complex and require the calculation of
Voronoi diagrams.
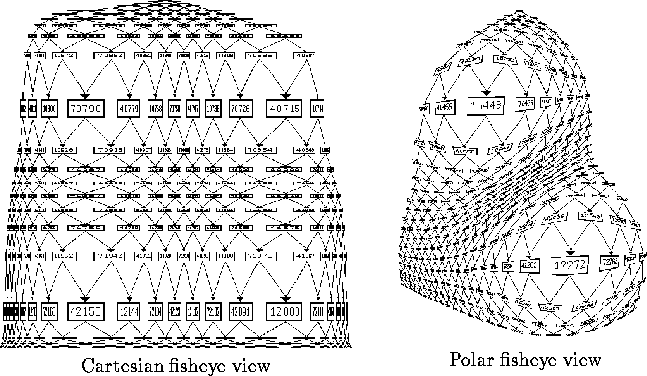
Figure 34: Fisheye Views with Two Focus Points
Another extension is the usage of multiple fisheye points [KRB95, MiSu91]. These are implemented by converting each display point of the graph once for every focus point and then taking the mathematical average of the transformed points as the picture location. Due to the special construction, superposition of two Cartesian views introduces two focus points but also two mirror focus points (Fig. 34). The mirror focus points are located an the further corners of the rectangle whose diagonal is given by the normal focus points. So there are four points where the magnification is maximal. This effect does not occur with polar fisheyes.