An enormous amount of theoretical and empirical research
effort has been devoted to decision under risk and decision
under uncertainty during the past few decades.
I comment here on two topics that illustrate very different facets of
this work.
Both have assumed that ![]() on X is a weak order.
The first is a theory of subjective expected utility that relaxes
continuity or an Archimedean axiom to obtain vector-valued
utilities ordered lexicographically along with subjective
probabilities characterized by real matrices rather than real numbers.
The second departs more radically from traditional theories and considers
the role of a binary operation
on X is a weak order.
The first is a theory of subjective expected utility that relaxes
continuity or an Archimedean axiom to obtain vector-valued
utilities ordered lexicographically along with subjective
probabilities characterized by real matrices rather than real numbers.
The second departs more radically from traditional theories and considers
the role of a binary operation ![]() of joint receipt.
The principal investigators are Irving LaValle in the
lexicographic domain and Duncan Luce for joint receipt.
of joint receipt.
The principal investigators are Irving LaValle in the
lexicographic domain and Duncan Luce for joint receipt.
The lexicographic story beings with Hausner's (1954) lexicographic
linear utility theory for a weak order ![]() on a mixture space X that can be viewed as a set of
lotteries or it's generalization for (7) that is
closed under a mixture operation.
Hausner assumed that
on a mixture space X that can be viewed as a set of
lotteries or it's generalization for (7) that is
closed under a mixture operation.
Hausner assumed that ![]() and
and ![]() satisfy independence
satisfy independence ![]() ;
;
![]() and proved that
and proved that
![]() is represented by a linear mapping into a real vector space
ordered lexicographically.
When the vector space has finite dimension, say
is represented by a linear mapping into a real vector space
ordered lexicographically.
When the vector space has finite dimension, say ![]() , this gives
, this gives
![]() that satisfies (7) along with
that satisfies (7) along with
where ![]() if the two vectors are not equal and
if the two vectors are not equal and
![]() for the smallest i at which they differ.
When
for the smallest i at which they differ.
When ![]() , (7) is
, (7) is
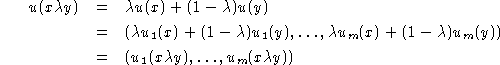
with each ![]() a linear functional on X.
We say that u is parsimonious of dimension m if the
representation can not be satisfied by any linear utility function of
smaller dimension.
Given that u is parsimonious of dimension m, it is unique up to an
affine transformation
a linear functional on X.
We say that u is parsimonious of dimension m if the
representation can not be satisfied by any linear utility function of
smaller dimension.
Given that u is parsimonious of dimension m, it is unique up to an
affine transformation
![]()
where v,u and ![]() are m-dimensional column vectors,
are m-dimensional column vectors, ![]() is
fixed, and G is an m-by-m lower triangular matrix (0's above the
main diagonal) with all diagonal entries positive.
is
fixed, and G is an m-by-m lower triangular matrix (0's above the
main diagonal) with all diagonal entries positive.
Failures of continuity that force ![]() in (7) and (11)
are analyzed in detail in Fishburn (1982).
The typical failure occurs when
in (7) and (11)
are analyzed in detail in Fishburn (1982).
The typical failure occurs when ![]() and
and ![]() for all
for all ![]() , in
which case there is a unique
, in
which case there is a unique ![]() such that
such that
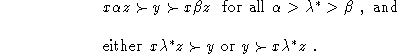
An example based on marginal probabilities is ![]() in which
in which ![]() is the probability of dying and
is the probability of dying and ![]() is the probability
that you or your heirs will receive $10.
If no increase in
is the probability
that you or your heirs will receive $10.
If no increase in ![]() can be compensated for by increasing
can be compensated for by increasing ![]() to 1,
then
to 1,
then ![]() can not be represented by a linear unidimensional
utility function,
but
can not be represented by a linear unidimensional
utility function,
but ![]() can represent
can represent ![]() lexicographically.
lexicographically.
The extension of linear lexicographic utility to decision under
uncertainty in LaValle and Fishburn (1991, 1992, 1996a) and Fishburn and LaValle (1993)
formulates X as the set of all finite-support probability distributions,
called mixed acts,
on a set A of acts in ![]() with
with ![]() .
In the main state-independent version of our theory, we assume
that every consequence is relevant for every state in S,
that the constant-act set
.
In the main state-independent version of our theory, we assume
that every consequence is relevant for every state in S,
that the constant-act set ![]() is included in A,
and that A has some additional structure.
We denote by
is included in A,
and that A has some additional structure.
We denote by ![]() the set of all lotteries on C and let
the set of all lotteries on C and let
![]() denote the marginal distribution in state i of
denote the marginal distribution in state i of ![]() .
.
The preference relation ![]() applies to X, and for p and q
in
applies to X, and for p and q
in ![]() ,
, ![]() means that
means that
![]() when
when ![]() and
and ![]() for every consequence
for every consequence ![]() .
We assume the following axioms:
.
We assume the following axioms:
![]() is a weak order,
is a weak order, ![]() and
and ![]() satisfy independence,
satisfy independence,
![]()
and a relaxed form of Archimedean axiom which implies that the
lexicographic hierarchy has only finitely many levels.
The axioms imply the existence of linear ![]() and
and ![]() that preserve lexicographically
that preserve lexicographically ![]() on X and
on X and ![]() on
on ![]() ,
respectively, with parsimonious dimension J of
,
respectively, with parsimonious dimension J of ![]() and K of u.
Because
and K of u.
Because ![]() on
on ![]() is tantamount to
the restriction of
is tantamount to
the restriction of ![]() on X to mixed constant acts, we have
on X to mixed constant acts, we have
![]() , and K < J if preferences between other acts force levels into
the hierarchy not accounted for by u on
, and K < J if preferences between other acts force levels into
the hierarchy not accounted for by u on ![]() .
Uniqueness follows the format described after (11).
.
Uniqueness follows the format described after (11).
Subjective matrix probabilities ![]() for
for ![]() rectify
rectify ![]() with
with ![]() in the expression
in the expression
![]()
where ![]() and
and ![]() are J-dimensional column vectors and
are J-dimensional column vectors and
![]() is a J-by-K real matrix that premultiplies the K-dimensional
column vector
is a J-by-K real matrix that premultiplies the K-dimensional
column vector ![]() .
Matrix
.
Matrix ![]() begins with
begins with ![]() nonzero columns followed by
nonzero columns followed by
![]() zero columns such that the first nonzero entry in
column k for
zero columns such that the first nonzero entry in
column k for ![]() is a positive number in row
is a positive number in row
![]() for some
for some ![]() .
In addition (LaValle and Fishburn 1996a),
.
In addition (LaValle and Fishburn 1996a), ![]() for some i,
for some i,
![]() for some i, and the J rows of the J-by-nK matrix
for some i, and the J rows of the J-by-nK matrix
![]() are linearly independent.
The resulting representation is
are linearly independent.
The resulting representation is
LaValle and Fishburn (1996b, 1996c) show how to assess the vector utilities and matrix probabilities in (12).
The latter paper also describes admissible transformations of the
matrix-probability distribution ![]() for any given u that put
for any given u that put ![]() in a standard normalized form.
With
in a standard normalized form.
With ![]() ,
we say that
,
we say that ![]() is a standard matrix distribution if
the K columns of
is a standard matrix distribution if
the K columns of ![]() are unit vectors
are unit vectors
![]() with the 1's in row positions
with the 1's in row positions
![]() left to right.
Thus, if K = J, then
left to right.
Thus, if K = J, then ![]() is the K-by-K identity matrix.
If K < J then standard
is the K-by-K identity matrix.
If K < J then standard ![]() has J-K rows of zeros
interspersed among the rows below row 1
of the K-by-K identity matrix.
has J-K rows of zeros
interspersed among the rows below row 1
of the K-by-K identity matrix.
Our second topic for decision under uncertainty is motivated by situations with holistic alternatives that consist of similar but clearly identifiable pieces received jointly, such as two checks and a bill in today's mail or the good news and bad news parts of a medical diagnosis. A fundamental behavioral question asks how people evaluate such alternatives for preference comparison or choice. Do they tend to combine similar pieces and then evaluate wholes, or do they evaluate pieces and then combine these evaluations to arrive at holistic assessments? And, in either case, what rules or operations govern the combining process?
To consider these questions, let ![]() denote a nonempty set of basic objects,
such as amounts of money or lotteries,
and let
denote a nonempty set of basic objects,
such as amounts of money or lotteries,
and let ![]() denote a binary operation of joint receipt that applies first
to
denote a binary operation of joint receipt that applies first
to ![]() and then to
and then to ![]() defined recursively by
defined recursively by
![]()
for ![]() , so that
, so that ![]() with limit
with limit ![]() .
We assume that
.
We assume that ![]() .
Then X includes at least one joint-receipt level.
We assume also that
.
Then X includes at least one joint-receipt level.
We assume also that ![]() on X is a weak order.
on X is a weak order.
An elementary case of joint receipt that does not involve decision under
risk or uncertainty takes ![]() with
with ![]() .
We interpret
.
We interpret ![]() as an amount of money and refer to
as an amount of money and refer to ![]() as a gain and to
as a gain and to ![]() as a loss.
An early empirical and partly theoretical study of joint receipt
for this case is Thaler (1985), followed by Thaler and
Johnson (1990) and Linville and Fischer (1991).
They focused in part on the hedonic editing rule
as a loss.
An early empirical and partly theoretical study of joint receipt
for this case is Thaler (1985), followed by Thaler and
Johnson (1990) and Linville and Fischer (1991).
They focused in part on the hedonic editing rule
where ![]() is strictly increasing, preserves
is strictly increasing, preserves ![]() , and has its
origin fixed by u(0) = 0.
This indicates pre-evaluation aggregation in u(x+y) as well as post-evaluation
aggregation in u(x) + u(y),
with addition as the combining operation in each case.
Thaler (1985) found that subjects tend to have
, and has its
origin fixed by u(0) = 0.
This indicates pre-evaluation aggregation in u(x+y) as well as post-evaluation
aggregation in u(x) + u(y),
with addition as the combining operation in each case.
Thaler (1985) found that subjects tend to have ![]() when x
and y are losses, but
when x
and y are losses, but ![]() when x and y are gains, and these agree with (13) if u is
convex
in losses and concave in gains.
Fishburn and Luce (1995) provides a complete analysis of (13)
under the assumption that u is convex in gains and either convex or concave in
losses.
The option for (13) is then clear except in the mixed loss and gain
region where x > 0 > y.
Our results for the mixed region, which depend on limiting slopes of u
at the origin and
when x and y are gains, and these agree with (13) if u is
convex
in losses and concave in gains.
Fishburn and Luce (1995) provides a complete analysis of (13)
under the assumption that u is convex in gains and either convex or concave in
losses.
The option for (13) is then clear except in the mixed loss and gain
region where x > 0 > y.
Our results for the mixed region, which depend on limiting slopes of u
at the origin and ![]() , show for most cases that there is a continuous
curve in
, show for most cases that there is a continuous
curve in ![]() that separates
that separates
![]() and
and ![]() when (13) holds.
when (13) holds.
Research that followed Thaler (1985) in Thaler and Johnson (1990), Linville and
Fischer (1991), and -- within a setting of certainty equivalents for
monetary lotteries -- in Luce (1995) and Cho and Luce (1996),
shows that (13) is not viable in many situations.
Part of the difficulty arises in the mixed region,
where individuals' assessments of
joint receipts are not generally well understood.
Another difficulty can be seen in the conjecture of Tversky and
Kahneman (1992) that ![]() , which was sustained at least in
the loss and gain regions separately in Cho and Luce (1996).
If
, which was sustained at least in
the loss and gain regions separately in Cho and Luce (1996).
If ![]() everywhere, it would gut (13) by
effectively excluding
everywhere, it would gut (13) by
effectively excluding ![]() .
Also, as Tversky and Kahneman (1992) notes, if in fact we assume that
.
Also, as Tversky and Kahneman (1992) notes, if in fact we assume that
![]() ,
as was done in part of Luce and Fishburn (1991), and if
,
as was done in part of Luce and Fishburn (1991), and if
![]() , then u(x) = kx for some k > 0, and
this linear form is supported neither by intuition nor by empirical research.
, then u(x) = kx for some k > 0, and
this linear form is supported neither by intuition nor by empirical research.
Empirical and theoretical investigations of joint receipt of lotteries or acts in decision under risk or uncertainty include, in addition to the certainty-equivalence approach of Luce (1995) and Cho and Luce (1996), Slovic and Lichtenstein (1968), Luce (1991), Luce and Fishburn (1991, 1995) and Cho, Luce and von Winterfeldt (1994). We comment briefly on representational aspects of Luce and Fishburn (1991, 1995) for a joint-receipt axiomatization of what they refer to as rank- and sign-dependent linear utility. A similar representation without the joint-receipt operation was proposed independently in Tversky and Kahneman (1992) and axiomatized in Wakker and Tversky (1993) under the rubric of cumulative prospect theory.
A central part of the representation in Luce and Fishburn (1991) is based on a
qualitative structure ![]() where
where ![]() is a weak order on X,
is a weak order on X, ![]() is a joint receipt operation on X, and e
denotes the status quo consequence.
Several axioms for the qualitative structure imply that there exists
is a joint receipt operation on X, and e
denotes the status quo consequence.
Several axioms for the qualitative structure imply that there exists
![]() that satisfies (1) along with u(e) = 0 and
that satisfies (1) along with u(e) = 0 and
where ![]() and
and ![]() are positive constants and
are positive constants and ![]() and
and ![]() are constants.
If u is unbounded and
are constants.
If u is unbounded and ![]() is monotonic in the sense that
is monotonic in the sense that ![]() and
and
![]() and
and ![]() and
and ![]() , then
, then
![]() and
and ![]() .
On the other hand, if
.
On the other hand, if ![]() and if u is bounded and
and if u is bounded and ![]() is monotonic, then (Luce and Fishburn 1995)
is monotonic, then (Luce and Fishburn 1995) ![]() and
and
![]() .
In both cases, if
.
In both cases, if ![]() is commutative and associative,
then
is commutative and associative,
then ![]() .
The weighted additive forms in (14) for the mixed cases of
.
The weighted additive forms in (14) for the mixed cases of ![]() and
and ![]() were
adopted as a compromise between
were
adopted as a compromise between ![]() and
more
complex possibilities.
and
more
complex possibilities.
To expand the formulation to the context of decision under uncertainty,
we can take ![]() as the set of all
acts in
as the set of all
acts in ![]() that assign only finite numbers of consequences to the
states, define
that assign only finite numbers of consequences to the
states, define ![]() as above, and assume that
as above, and assume that ![]() is associative so that
is associative so that ![]() can be replaced by the set
can be replaced by the set ![]() of all finite sequences
of all finite sequences ![]() for which
for which ![]() and
and ![]() for all i.
Representation (14) applies under this expansion with
for all i.
Representation (14) applies under this expansion with
![]() .
Given X in this form, Luce and Fishburn (1991) describes conditions
which imply algebraic forms for the utility of acts that
involve subjective probabilities.
We illustrate with
.
Given X in this form, Luce and Fishburn (1991) describes conditions
which imply algebraic forms for the utility of acts that
involve subjective probabilities.
We illustrate with ![]() ,
as in a monetary context, with
,
as in a monetary context, with ![]() increasing in c.
increasing in c.
Let cEd denote the act in ![]() that yields c if event
that yields c if event
![]() obtains and yields d otherwise.
Assuming that E is neither empty nor the universal event and that
e = 0 with u(0) = 0,
one form is
obtains and yields d otherwise.
Assuming that E is neither empty nor the universal event and that
e = 0 with u(0) = 0,
one form is
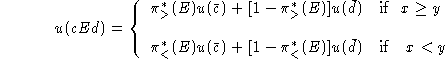
with ![]() .
This applies separately to gains, where
.
This applies separately to gains, where ![]() and
and
![]() , and to losses, where
, and to losses, where ![]() and
and ![]() .
.
For each ![]() , let
, let ![]() and
and ![]() ,
and define
,
and define ![]() by
by

A main part of the representation in Luce and Fishburn (1991) separates gains from losses in the decomposition
![]()
with ![]() for
for ![]() and
and ![]() ,
and with the
,
and with the ![]() unique
and u unique up to a proportionality transform that fixes u(e) at 0.
Additional conditions that allow further refinements for
unique
and u unique up to a proportionality transform that fixes u(e) at 0.
Additional conditions that allow further refinements for ![]() and
and ![]() based on (14) are described in the reference.
based on (14) are described in the reference.
Luce and Fishburn (1995) focuses on the monetary context with
e = 0 and considers first the effect of ![]() for monetary amounts with
for monetary amounts with ![]() monotonic.
We adopt the first and last lines of (14) for joint gains and
joint losses respectively, so that:
monotonic.
We adopt the first and last lines of (14) for joint gains and
joint losses respectively, so that:
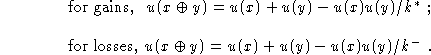
We assume ![]() and
and ![]() , which imply u(x+y) < u(x) + u(y)
for gains and u(x+y ) > u(x) + u(y) for losses, given
, which imply u(x+y) < u(x) + u(y)
for gains and u(x+y ) > u(x) + u(y) for losses, given
![]() .
These inequalities are consistent with studies, including Kahneman and
Tversky (1979) and others surveyed in Fishburn and Kochenberger (1979), that observe
increasing marginal utility for losses and decreasing marginal
utility for gains.
We show in Luce and Fishburn (1995) that these hypotheses imply exponential
expressions for utility of gains and utility of losses:
.
These inequalities are consistent with studies, including Kahneman and
Tversky (1979) and others surveyed in Fishburn and Kochenberger (1979), that observe
increasing marginal utility for losses and decreasing marginal
utility for gains.
We show in Luce and Fishburn (1995) that these hypotheses imply exponential
expressions for utility of gains and utility of losses:
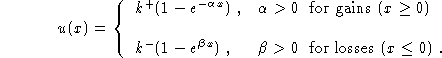
We also consider lotteries without presuming ![]() but maintaining the parts of (14) just noted.
Let x denote a lottery on gains
but maintaining the parts of (14) just noted.
Let x denote a lottery on gains
![]() with
with ![]() and
and
![]() .
We identify fairly reasonable assumptions which imply the rank-dependent
form (Quiggin 1993)
.
We identify fairly reasonable assumptions which imply the rank-dependent
form (Quiggin 1993)
![]()
in which ![]() and
and ![]() is a continuous
and increasing map
from [0,1] onto [0,1].
A similar form with
is a continuous
and increasing map
from [0,1] onto [0,1].
A similar form with ![]() in place of
in place of ![]() applies to lotteries
on losses.
The issue of mixed gains and losses is more problematic as
described in Section 5 in Luce and Fishburn (1995).
applies to lotteries
on losses.
The issue of mixed gains and losses is more problematic as
described in Section 5 in Luce and Fishburn (1995).